use OpenGL;
#5 KappaTau Space Curves
The shape of a space curve is well defined by its curvature (greek letter kappa)
and its torsion (greek letter tau) according to the parameter s, the arclength.
Rudy Rucker calls Kappatau curve such a curve in his paper:
How Flies Fly: Kappatau Space Curves.
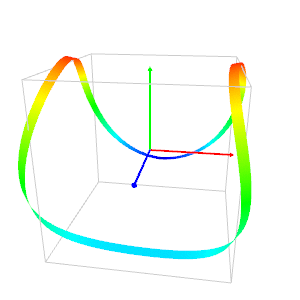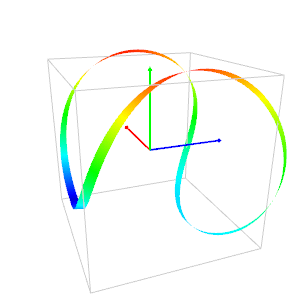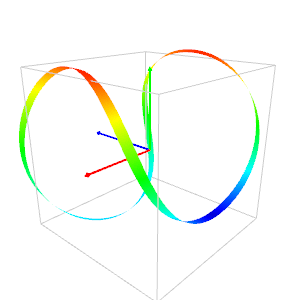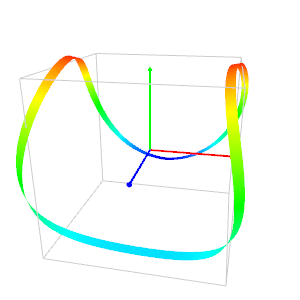
The program below plots a curve called "rocker" by Rudy Rucker (first image).
He calls "phone-cord" the curve of the second image (In ancient times the phones had cords!).
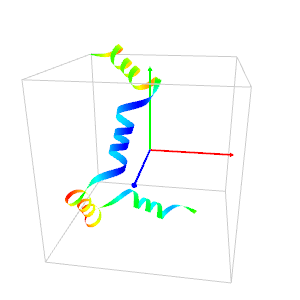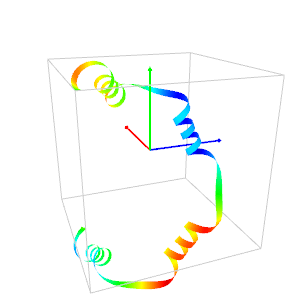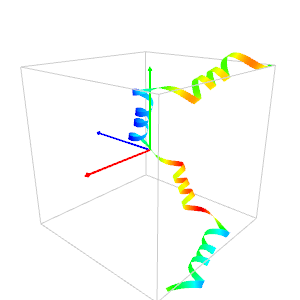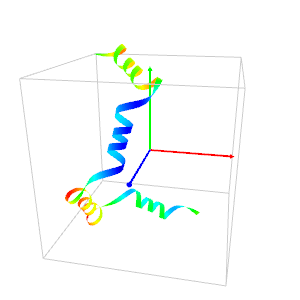
rocker.pl
#!/usr/local/bin/perl
#
# rocker.pl : draw a KappaTau curve
# (c) 2013 jl_morel@bribes.org - http://http://bribes.org/perl
use strict;
use warnings;
use OpenGL qw/ :all /;
use Math::Trig;
#------ Base vectors
my @i = ( 1, 0, 0 );
my @j = ( 0, 1, 0 );
my @k = ( 0, 0, 1 );
my @O = ( 0, 0, 0 ); #origin
#------ Initialization
my $s = 0; # Natural parameter s (arclength)
my $smax = 4 * pi;
my $ds = 0.0001; # s increment
my $width = 0.1; # Frenet ribbon width
my @P = ( 0, -0.5, -1 ); # Starting point
my @T = @i; # initial Frenet-Serret frame
my @N = @j;
my @B = @k;
my $curve; # OpenGL display list for the curve
sub kappa { # curvature function
my $s = shift;
return 1;
}
sub tau { # torsion function
my $s = shift;
return sin $s;
}
#------ NextPoint
# Calculates the next point P(s+ds) from P(s) using the Frenet–Serret formulas
sub NextPoint {
@P = AddVectors( @P, ScaleVector( @T, $ds ) );
$s += $ds;
@T = AddVectors( @T, ScaleVector( @N, kappa($s) * $ds ) );
@B = AddVectors( @B, ScaleVector( @N, -tau($s) * $ds ) );
@T = NormalizeVector(@T);
@B = NormalizeVector(@B);
@N = CrossProduct( @B, @T );
}
#------ DrawCurve
# Returns an OpenGL display list of the curve
sub DrawCurve {
my $curve = glGenLists(1);
glNewList( $curve, GL_COMPILE );
my @P0 = @P; # initialization
my @R0 = AddVectors( @P, ScaleVector( @B, $width ) );
glBegin(GL_TRIANGLES);
for ( my $i = 1 ; $i <= $smax / $ds ; $i++ ) {
NextPoint();
if ( $i % 100 == 0 ) { # we draw only every 100 points
my @R = AddVectors( @P, ScaleVector( @B, $width ) );
# We colorize with the angle (@N, @j) (mod pi)
glColor3f( Rainbow( 1 / pi * acos DotProduct( @N, @j ) ) );
# The quadrilateral @P0 @R0 @R @P is not a Quad
glVertex3f(@P0); # we draw the triangle @P0 @R0 @R
glVertex3f(@R0);
glVertex3f(@R);
glVertex3f(@P0); # then the triangle @P0 @R @P
glVertex3f(@R);
glVertex3f(@P);
@P0 = @P; # save for next step
@R0 = @R;
}
}
glEnd();
glEndList;
return $curve;
}
#------ Initialization routine
sub init {
glClearColor( 1, 1, 1, 1 ); # White background
glEnable(GL_DEPTH_TEST); # Enable hidden surface removal
glEnable(GL_MULTISAMPLE); # Enable multisample antialiasing
$curve = DrawCurve();
}
#------ Draw the scene
my $spin = 0.0;
sub display {
glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );
glLoadIdentity();
gluLookAt( 2.0, 4.0, 10.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0 );
glPushMatrix();
glScalef( 2.5, 2.5, 2.5 );
glRotatef( $spin, 0.0, 1.0, 0.0 );
DrawAxes(0.5); # Axes
glColor3f( 0.8, 0.8, 0.8 );
glutWireCube(2); # Gray wired cube
glCallList($curve); # Curve
glPopMatrix();
glutSwapBuffers();
# debug code
# if ( ( my $e = glGetError() ) != GL_NO_ERROR ) {
# print "error : ", gluErrorString($e), "\n";
# }
}
#------ GLUT Callback called when the window is resized
sub reshape {
my ( $w, $h ) = @_;
glViewport( 0, 0, $w, $h );
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective( 45.0, $h ? $w / $h : 0, 1.0, 20.0 );
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
#------ Routine for rotating the scene
my $WaitUntil = 0;
sub spinDisplay {
my $TimeNow = glutGet(GLUT_ELAPSED_TIME);
if ( $TimeNow >= $WaitUntil ) {
$spin += 1.0;
$spin = $spin - 360.0 if ( $spin > 360.0 );
glutPostRedisplay();
$WaitUntil = $TimeNow + 1000 / 25; # 25 frames/s
}
}
#------ Main
glutInit();
glutInitDisplayMode(
GLUT_DOUBLE # Double buffering
| GLUT_RGB # RGB mode
| GLUT_DEPTH # Hidden surface removal
| GLUT_MULTISAMPLE # Multisample antialiasing
);
glutInitWindowPosition( 0, 0 );
glutInitWindowSize( 300, 300 );
glutCreateWindow("KappaTau curve");
init();
glutDisplayFunc( \&display );
glutReshapeFunc( \&reshape );
glutMouseFunc( \&mouse );
glutIdleFunc( \&spinDisplay );
glutMainLoop();
# ============ Some auxiliary routines
#------ Returns the cross product of 2 vectors
sub CrossProduct {
return (
$_[1] * $_[5] - $_[2] * $_[4],
$_[3] * $_[2] - $_[0] * $_[5],
$_[0] * $_[4] - $_[1] * $_[3]
);
}
#------ Returns the dot product of 2 vectors
sub DotProduct {
return $_[0] * $_[3] + $_[1] * $_[4] + $_[2] * $_[5];
}
#------ Returns the length of a vector
sub GetVectorLength {
return sqrt( $_[0] * $_[0] + $_[1] * $_[1] + $_[2] * $_[2] );
}
#------ Returns the sum of 2 vectors
sub AddVectors {
return ( $_[0] + $_[3], $_[1] + $_[4], $_[2] + $_[5] );
}
#------ Returns the vector scaled by the last parameter
sub ScaleVector {
return ( $_[0] * $_[3], $_[1] * $_[3], $_[2] * $_[3] );
}
#------ Returns a normalized vector (length = 1)
sub NormalizeVector {
return ( 0, 0, 0 ) if ( my $norm = GetVectorLength(@_) ) == 0;
return ScaleVector( @_, 1 / $norm );
}
#------ DrawArrow
# Usage: DrawArrow( @A, @V [,$k] );
# Draws an arrow representing the vector @V with the point @A as origin.
# The optional parameter scales the arrow thickness (default to 1).
sub DrawArrow {
my ( $ox, $oy, $oz, $x, $y, $z, $k ) = @_;
$k ||= 1;
my $norm = GetVectorLength( $x, $y, $z );
my @u = NormalizeVector( $x, $y, $z );
my @v = CrossProduct( @k, @u );
my $alpha = rad2deg acos DotProduct( @k, @u );
my $CylinderRadius = 0.025 * $k;
my $ConeHeight = 0.1 * $k;
my $ConeRadius = 0.06 * $k;
my $CylinderHeight = $norm - $ConeHeight;
# Setup the quadric object
my $Qobj = gluNewQuadric();
gluQuadricDrawStyle( $Qobj, GLU_FILL );
gluQuadricNormals( $Qobj, GLU_SMOOTH );
gluQuadricOrientation( $Qobj, GLU_OUTSIDE );
gluQuadricTexture( $Qobj, GL_FALSE );
glPushMatrix();
glTranslatef( $ox, $oy, $oz );
glRotatef( $alpha, @v );
gluCylinder( $Qobj, $CylinderRadius, $CylinderRadius, $CylinderHeight, 10, 1 );
glPushMatrix();
gluDisk( $Qobj, 0, $CylinderRadius, 10, 1 );
glTranslatef( 0.0, 0.0, $CylinderHeight );
gluCylinder( $Qobj, $ConeRadius, 0.0, $ConeHeight, 10, 1 );
glRotatef( 180, @j );
gluDisk( $Qobj, $CylinderRadius, $ConeRadius, 10, 1 );
glPopMatrix();
glPopMatrix();
}
#------ DrawAxes
# Usage: DrawAxes( [$k] );
# Draws the unit vectors of the cartesian coordinates system at the origine O.
# The optional parameter scales the arrow thickness (default to 1).
sub DrawAxes {
my $k = shift;
glColor3f(@i);
DrawArrow( @O, @i, $k );
glColor3f(@j);
DrawArrow( @O, @j, $k );
glColor3f(@k);
DrawArrow( @O, @k, $k );
}
#------ Rainbow color map function
# Usage: ($red, $green, $blue) = Rainbow( $x );
# $x must be between 0 and 1.
# Returns the color of the rainbow (RGB list) associated with $x
# from blue for $x = 0 to red for $x = 1.
sub max { $_[0] < $_[1] ? $_[1] : $_[0] } # max auxiliary function
sub Rainbow {
my $dx = 0.8;
my $s = ( 6 - 2 * $dx ) * $_[0] + $dx;
return max( 0, ( 3 - abs( $s - 4 ) - abs( $s - 5 ) ) / 2 ), # Red
max( 0, ( 4 - abs( $s - 2 ) - abs( $s - 4 ) ) / 2 ), # Green
max( 0, ( 3 - abs( $s - 1 ) - abs( $s - 2 ) ) / 2 ); # Blue
}
The script as .txt for download:
rocker.pl.txt
Back to Top
BðP © 2013 J-L Morel - Contact : jl_morel@bribes.org
![[Validation HTML 4.0!]](vh401.gif)

