use OpenGL;
#4 Arrows
This program illustrates the use of 3D arrows with OpenGL.
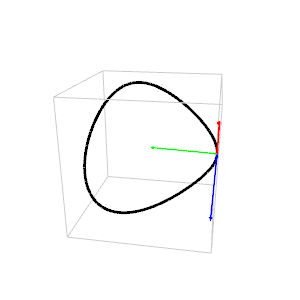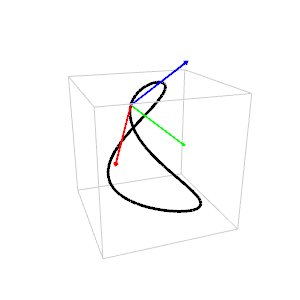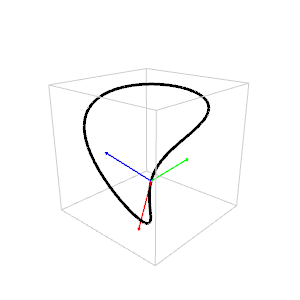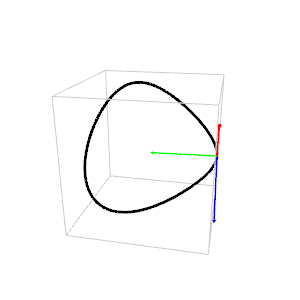
The animation shows the
Frenet-Serret trihedron moving along a space curve.
The tangent is red, the normal green and the binormal blue.
The curve has no universal name. In French it is
"la courbe de la crêpe".

arrows.pl
#!/usr/local/bin/perl
#
# arrows.pl : 3D arrows with OpenGL.
# (c) 2013 jl_morel@bribes.org - http://http://bribes.org/perl
use strict;
use warnings;
use OpenGL qw/ :all /;
use Math::Trig;
# ============ Some 3D math routines
#------ Returns the cross product of 2 vectors
sub CrossProduct {
return (
$_[1] * $_[5] - $_[2] * $_[4],
$_[3] * $_[2] - $_[0] * $_[5],
$_[0] * $_[4] - $_[1] * $_[3]
);
}
#------ Returns the dot product of 2 vectors
sub DotProduct {
return $_[0] * $_[3] + $_[1] * $_[4] + $_[2] * $_[5];
}
#------ Returns the length of a vector
sub GetVectorLength {
return sqrt( $_[0] * $_[0] + $_[1] * $_[1] + $_[2] * $_[2] );
}
#------ Returns the vector scaled by the last parameter
sub ScaleVector {
return ( $_[0] * $_[3], $_[1] * $_[3], $_[2] * $_[3] );
}
#------ Returns a normalized vector (length = 1)
sub NormalizeVector {
return ( 0, 0, 0 ) if ( my $norm = GetVectorLength(@_) ) == 0;
return ScaleVector( @_, 1 / $norm );
}
#------ Base vectors
my @i = ( 1, 0, 0 ); # this vector is red!
my @j = ( 0, 1, 0 ); # this vector is green!
my @k = ( 0, 0, 1 ); # this vector is blue!
my @O = ( 0, 0, 0 ); # origin
#============ End math routines
#------ DrawArrow
# Usage: DrawArrow( @A, @V [,$k] );
# Draws an arrow representing the vector @V with the point @A as origin.
# The optional parameter scales the arrow thickness (default to 1).
sub DrawArrow {
my ( $ox, $oy, $oz, $x, $y, $z, $k ) = @_;
$k ||= 1;
my $norm = GetVectorLength( $x, $y, $z );
my @u = NormalizeVector( $x, $y, $z );
my @v = CrossProduct( @k, @u );
my $alpha = rad2deg acos DotProduct( @k, @u );
my $CylinderRadius = 0.025 * $k;
my $ConeHeight = 0.1 * $k;
my $ConeRadius = 0.06 * $k;
my $CylinderHeight = $norm - $ConeHeight;
# Setup the quadric object
my $Qobj = gluNewQuadric();
gluQuadricDrawStyle( $Qobj, GLU_FILL );
gluQuadricNormals( $Qobj, GLU_SMOOTH );
gluQuadricOrientation( $Qobj, GLU_OUTSIDE );
gluQuadricTexture( $Qobj, GL_FALSE );
glPushMatrix();
glTranslatef( $ox, $oy, $oz );
glRotatef( $alpha, @v );
gluCylinder( $Qobj, $CylinderRadius, $CylinderRadius, $CylinderHeight, 10, 1 );
glPushMatrix();
gluDisk( $Qobj, 0, $CylinderRadius, 10, 1 );
glTranslatef( 0, 0, $CylinderHeight );
gluCylinder( $Qobj, $ConeRadius, 0, $ConeHeight, 10, 1 );
glRotatef( 180, @j );
gluDisk( $Qobj, $CylinderRadius, $ConeRadius, 10, 1 );
glPopMatrix();
glPopMatrix();
}
#------ DrawArrow2Points
# Usage: DrawArrow( @A, @B [,$k] );
# Draws an arrow connecting an initial point @A with a terminal point @B.
# The optional parameter scales the arrow thickness (default to 1).
sub DrawArrow2Points {
my ( $ax, $ay, $az, $bx, $by, $bz, $k ) = @_;
DrawArrow( $ax, $ay, $az, $bx - $ax, $by - $ay, $bz - $az, $k );
}
#------ DrawAxes
# Usage: DrawAxes( [$k] );
# Draws the unit vectors of the cartesian coordinates system at the origine O.
# The optional parameter scales the arrow thickness (default to 1).
sub DrawAxes {
my $k = shift;
glColor3f(@i); # red
DrawArrow( @O, @i, $k );
glColor3f(@j); # green
DrawArrow( @O, @j, $k );
glColor3f(@k); # blue
DrawArrow( @O, @k, $k );
}
# ------ La "courbe de la crêpe"
# http://www.mathcurve.com/courbes3d/crepe/crepe.shtml
sub R {
my $t = shift;
return cos $t, sin $t, 0.5 * sin 2 * $t;
}
#--- First derivative
sub Rp {
my $t = shift;
return -sin $t, cos $t, cos 2 * $t;
}
#--- Second derivative
sub Rs {
my $t = shift;
return -cos $t, -sin $t, -2 * sin 2 * $t;
}
#------ Draw the Frenet–Serret frame (Moving trihedron)
sub DrawSerretFrenet {
my ( $t, $k ) = @_;
my @R = R($t);
my @T = NormalizeVector( Rp($t) ); # tangent
glColor3f(@i); # red
DrawArrow( @R, @T, $k );
my @B = CrossProduct( @T, Rs($t) );
@B = NormalizeVector(@B); # binormal
glColor3f(@k); # blue
DrawArrow( @R, @B, $k );
my @N = CrossProduct( @B, @T ); # normal
glColor3f(@j); # green
DrawArrow( @R, @N, $k );
}
#------ Initialization routine
sub init {
glClearColor( 1, 1, 1, 1 );
glShadeModel(GL_SMOOTH); # Smooth shading
glEnable(GL_DEPTH_TEST); # Enable hidden surface removal
glEnable(GL_MULTISAMPLE); # Enable multisample antialiasing
}
#------ Draw the scene
my $spin = 0;
my $t = 0;
sub display {
glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );
glLoadIdentity();
gluLookAt( 2.0, 4.0, 10.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0 );
glPushMatrix();
glScalef( 2.0, 2.0, 2.0 );
glRotatef( $spin, 0.0, 1.0, 0.0 );
glColor3f( 0.8, 0.8, 0.8 ); # draw the cube in gray
glLineWidth(1);
glutWireCube(2);
glColor3f( 0, 0, 0 ); # draw the curve in black
glLineWidth(3);
glBegin(GL_LINE_STRIP);
for ( my $i = 0 ; $i <= 360 ; $i += 5 ) {
glVertex3f( R( deg2rad($i) ) );
}
glEnd();
DrawSerretFrenet( deg2rad($t), 0.5 ); #draw the frame
glPopMatrix();
glutSwapBuffers();
# debug code
# if ( ( my $e = glGetError() ) != GL_NO_ERROR ) {
# print "error : ", gluErrorString($e), "\n";
# }
}
#------ GLUT Callback called when the window is resized
sub reshape {
my ( $w, $h ) = @_;
glViewport( 0, 0, $w, $h );
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective( 45.0, $h ? $w / $h : 0, 1.0, 20.0 );
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
#------ Routine for rotating the scene
my $WaitUntil = 0;
sub spinDisplay {
my $TimeNow = glutGet(GLUT_ELAPSED_TIME);
if ( $TimeNow >= $WaitUntil ) {
$spin += 1.0;
$spin = $spin - 360.0 if ( $spin > 360.0 );
$t += 1;
$t = 0 if $t > 360;
glutPostRedisplay();
$WaitUntil = $TimeNow + 1000 / 25; # 25 frames/s
}
}
#------ Main
glutInit();
glutInitDisplayMode(
GLUT_DOUBLE # Double buffering
| GLUT_RGB # RGB mode
| GLUT_DEPTH # Hidden surface removal
| GLUT_MULTISAMPLE # Multisample antialiasing
);
glutInitWindowSize( 300, 300 );
glutCreateWindow("Serret-Frenet frame");
init();
glutDisplayFunc( \&display );
glutReshapeFunc( \&reshape );
glutIdleFunc( \&spinDisplay );
glutMainLoop();
The script as .txt for download:
arrows.pl.txt
Back to Top
BðP © 2013 J-L Morel - Contact : jl_morel@bribes.org
![[Validation HTML 4.0!]](vh401.gif)

