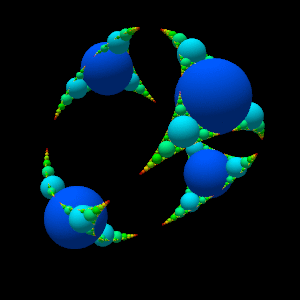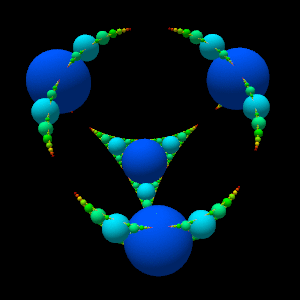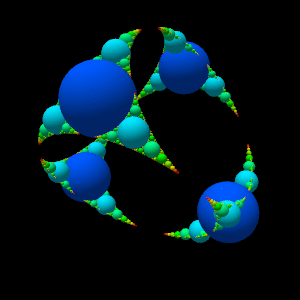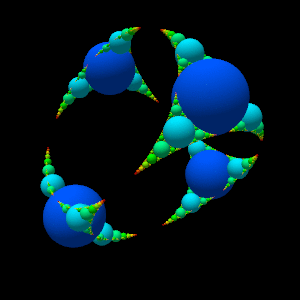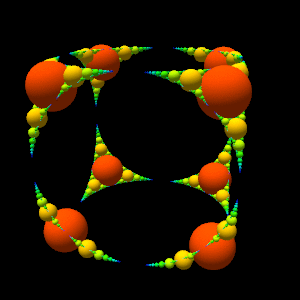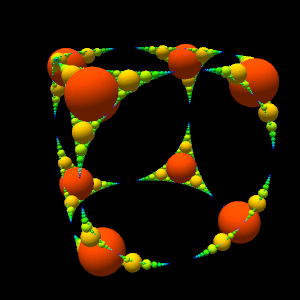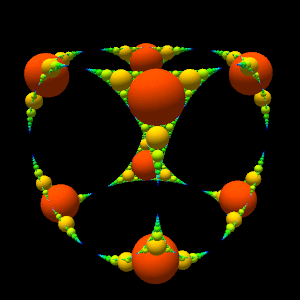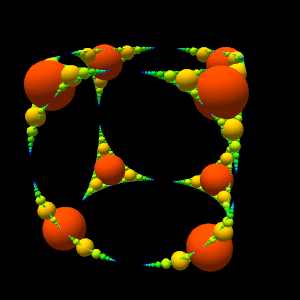use OpenGL;
#9 Spherical Apollonian gasket
This program draws a spherical
Apollonian gasket .
The difficulty is to determine the center of the Apollonius circle of three tangent circles in space.
I treat this as an optimization problem. The
Gradient descent
permits to find a point equidistant
from the three circles (This is my way of doing it, you will not find it in a geometry book!).
In the last two images, the circles are replaced by spheres to give more relief.

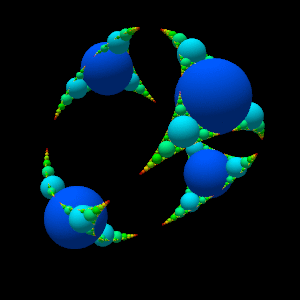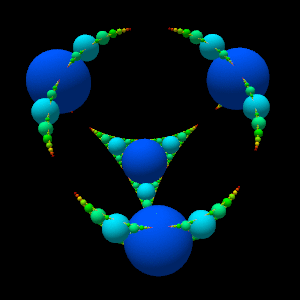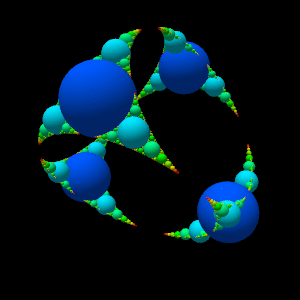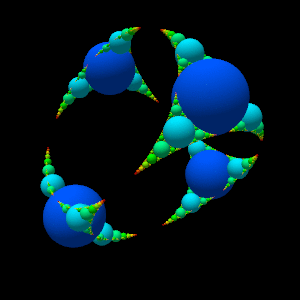
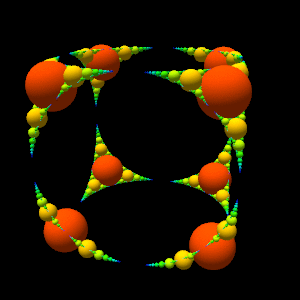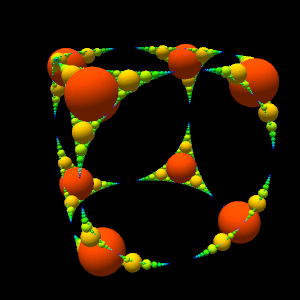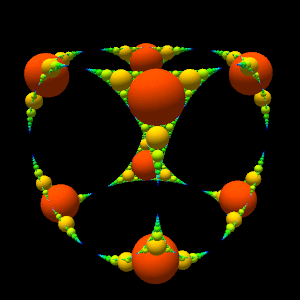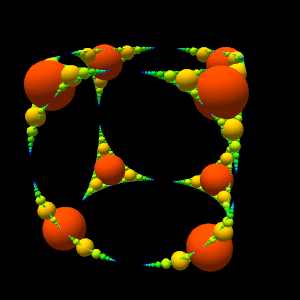
apollonius.pl
#!/usr/local/bin/perl
#
# apollonius.pl : Draws a 3D Apollonius gasket
# (c) 2013 jl_morel@bribes.org - http://http://bribes.org/perl
use strict;
use warnings;
use OpenGL qw/ :all /;
use Math::Trig;
use Carp;
#------ Base vectors
my @i = ( 1, 0, 0 );
my @j = ( 0, 1, 0 );
my @k = ( 0, 0, 1 );
my @O = ( 0, 0, 0 );
#------ Circle closest point
# ClosestPointC( @P, @C );
# Returns the closest point of the circle @C to the point @P
sub ClosestPointC {
my @P = @_[0..2]; # point P
my @C = @_[3..5]; # circle center
my @N = @_[6..8]; # normal vector
my $r = $_[9]; # circle radius
my @M = CrossProduct( @N, CrossProduct(SubVectors(@P, @C), @N) );
@M = ScaleVector(NormalizeVector(@M), $r);
return AddVectors(@C, @M);
}
#------ Distance from a point to a circle
# DistPC( @P, @C );
# Returns the distance between a point @P and a circle @C
sub DistPC {
my @P = @_[0..2]; # the point
my @C = @_[3..9]; # the circle
return Dist(@P, ClosestPointC(@P, @C));
}
#------ Objective function (cost function)
# The minimum of this positive function is zero.
# At this minimum, the point P is equidistant of the three circles.
sub ObjectiveFunction {
my @P = @_[0..2]; # the point
my @C1 = @_[3..9]; # the three circles
my @C2 = @_[10..16];
my @C3 = @_[17..23];
my $d1 = DistPC(@P, @C1);
my $d2 = DistPC(@P, @C2);
my $d3 = DistPC(@P, @C3);
return ($d1-$d2)**2+($d2-$d3)**2+($d3-$d1)**2;
}
#------ FindEquid
# Being given three pairwise externally tangent circles on the sphere
# of center O, and a good guess point, this function returns
# a point P equidistant from the three circles.
# We use the gradient descent to find the local minimum of the previous
# objective function.
sub FindEquid {
my @P = @_[0..2]; # guess point
my @C1 = @_[3..9]; # the three circles
my @C2 = @_[10..16];
my @C3 = @_[17..23];
# $theta and $phi are the spherical coordinates of P
@P = NormalizeVector(@P);
my $phi = acos($P[2]);
my $theta = acos($P[0]/sqrt($P[0]*$P[0]+$P[1]*$P[1]));
$theta = -$theta if $P[1]<0;
my $f = ObjectiveFunction(@P, @C1, @C2, @C3);
my $ds = 1e-4;
while ( $f > 1e-6 ) {
# derivative of f with respect to theta and phi
my $dft = (ObjectiveFunction(cos($theta+$ds)*sin($phi),
sin($theta+$ds)*sin($phi),
cos($phi), @C1, @C2, @C3)-$f)/$ds;
my $dfp = (ObjectiveFunction(cos($theta)*sin($phi+$ds),
sin($theta)*sin($phi+$ds),
cos($phi+$ds) , @C1, @C2, @C3)-$f)/$ds;
my $k = 0.1;
my ($thetaN, $phiN, $fN); # New (and better!) values of ...
$thetaN = $theta - $k*$dft;
$phiN = $phi - $k*$dfp;
$fN = ObjectiveFunction(cos($thetaN)*sin($phiN),
sin($thetaN)*sin($phiN),
cos($phiN) , @C1, @C2, @C3);
$theta = $thetaN;
$phi = $phiN;
@P = ( cos($theta)*sin($phi), sin($theta)*sin($phi), cos($phi) );
$f = ObjectiveFunction(@P, @C1, @C2, @C3);
}
return @P;
}
#------ FindApolloniusCircle
# Returns the Apollonius circle of three pairwise externally tangent circles
# on a sphere of center O.
sub FindApolloniusCircle {
my @C1 = @_[0..6]; # the three circles
my @C2 = @_[7..13];
my @C3 = @_[14..20];
# if one of the circles is too small then the Apollonius circle is too
# small too and we do not draw small circles!
return @C1 if ( $C1[-1] < 0.001 );
return @C2 if ( $C2[-1] < 0.001 );
return @C3 if ( $C3[-1] < 0.001 );
# points of tangency
my @T12 = ClosestPointC( @C1[0..2], @C2);
my @T13 = ClosestPointC( @C2[0..2], @C3);
my @T23 = ClosestPointC( @C3[0..2], @C1);
# we take as guess point the centroid of the points of tangency
# (the centroid of the centers of the three circles is not a good guess point)
my @P = GetBaryCenter( @T12, 1, @T13, 1, @T23, 1);
@P = FindEquid(@P, @C1, @C2, @C3); # @P is equidistant of the circles
# points of tangency of the Apollonius circle
my @P1 = ClosestPointC( @P, @C1);
my @P2 = ClosestPointC( @P, @C2);
my @P3 = ClosestPointC( @P, @C3);
return GetCircumCircle(@P1, @P2, @P3);
}
#------ Initializations
#--- the four vertices of the tetrahedron
my @S1 = (1, -1, -1);
my @S2 = (1, 1, 1);
my @S3 = (-1, -1, 1);
my @S4 = (-1, 1, -1);
#--- the three base circles
my @C0 = GetInCircle(@S1, @S2, @S3);
my @C1 = GetInCircle(@S1, @S2, @S4);
my @C2 = GetInCircle(@S3, @S2, @S4);
my @C3 = FindApolloniusCircle(@C0, @C1, @C2);
#--- @gasket is the list of circles to draw
my @gasket = ( [@C0], # circle C0
[@C1], # circle C1
[@C2], # circle C2
[@C3] # Apollonius Circle of C0, C1, C2
);
#--- @triads is a list of list of the indices of a triad of circles and
# its Apollonius circle.
my @triads = ([0, 1, 2, 3]); # the first triad at level 0
#--- %indexcolor is a hash whose keys are indexes where the level changes
my %indexcolor;
$indexcolor{4} = 1;
#------ triad iterator
sub nextstep {
my @old_triads = @_;
my $last_index = 1+$old_triads[-1]->[-1];
$indexcolor{$last_index} = 1;
my @next_triads;
foreach my $t ( @old_triads ) {
push @next_triads, [$t->[0], $t->[1], $t->[3], $last_index++];
push @next_triads, [$t->[1], $t->[2], $t->[3], $last_index++];
push @next_triads, [$t->[2], $t->[0], $t->[3], $last_index++];
}
return @next_triads;
}
#------ Initialization routine
my $gasket_corner; # OpenGL display list for one corner of the gasket
my $levelmax = 8; # Number of iterations
sub init {
glClearColor(0, 0, 0, 1 ); # Black background
glShadeModel(GL_SMOOTH); # Smooth shading
glEnable(GL_MULTISAMPLE); # Enable multisample antialiasing
glEnable(GL_DEPTH_TEST); # Enable hidden surface removal
# Generating the list of circles
for (1..$levelmax) {
@triads = nextstep @triads;
foreach my $t ( @triads ) {
$gasket[$t->[3]] = [ FindApolloniusCircle(@{$gasket[$t->[0]]},
@{$gasket[$t->[1]]},
@{$gasket[$t->[2]]}) ];
}
}
# Compilation of the display list
$gasket_corner = glGenLists(1);
glNewList( $gasket_corner, GL_COMPILE );
my $i = 0; # Current index of the circle to draw
my $level = 0; # Current level
foreach (@gasket) {
$level++ if exists $indexcolor{$i++};
glColor3f( Rainbow($level/($levelmax+1)) );
if ( @{$_}[-1] > 0.001 ) { # One does not draw small circles
my $r = @{$_}[-1] - 0.001; # Compensation line thickness
DrawCircle(@{$_}[0..5], $r, 0.002);
}
}
glEndList();
}
#------ Draw the scene
my $spin = 0;
sub display {
glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );
glLoadIdentity();
gluLookAt( 2.0, 4.0, 10.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0 );
glPushMatrix();
my $scale = 3.8;
glScalef( $scale, $scale, $scale );
glRotatef( $spin, 0.0, 1.0, 0.0 );
# draws the complete gasket using symmetries
glCallList($gasket_corner);
glRotatef( 180, @i );
glCallList($gasket_corner);
glRotatef( 180, @j );
glCallList($gasket_corner);
glRotatef( 180, @i );
glCallList($gasket_corner);
glPopMatrix();
glutSwapBuffers();
}
#------ GLUT Callback called when the window is resized
sub reshape {
my ( $w, $h ) = @_;
glViewport( 0, 0, $w, $h );
glMatrixMode(GL_PROJECTION);
glLoadIdentity(); # define the projection
gluPerspective( 45.0, $h ? $w / $h : 0, 1.0, 20.0 );
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
}
#------ Routine for rotating the scene
my $WaitUntil = 0;
sub spinDisplay {
my $TimeNow = glutGet(GLUT_ELAPSED_TIME);
if ( $TimeNow >= $WaitUntil ) {
$spin += 1.0;
$spin = $spin - 360.0 if ( $spin > 360.0 );
glutPostRedisplay();
$WaitUntil = $TimeNow + 1000 / 25; # 25 frames/s
}
}
#------ GLUT callback for the mouse
sub mouse {
my ( $button, $state, $x, $y ) = @_;
if ( $button == GLUT_LEFT_BUTTON ) {
glutIdleFunc( \&spinDisplay ) if ( $state == GLUT_DOWN );
}
elsif ( $button == GLUT_RIGHT_BUTTON ) {
glutIdleFunc(undef) if ( $state == GLUT_DOWN );
}
}
#------ Main program
glutInit();
glutInitDisplayMode(
GLUT_DOUBLE # Double buffering
| GLUT_RGB # RGB color mode
| GLUT_DEPTH # Hidden surface removal
| GLUT_MULTISAMPLE # Multisample antialiasing
);
glutInitWindowSize( 300, 300 );
glutCreateWindow("Circles");
init();
glutDisplayFunc( \&display );
glutReshapeFunc( \&reshape );
glutMouseFunc( \&mouse );
glutIdleFunc( \&spinDisplay );
glutMainLoop();
# ====== Utility Functions
#------ Add two vectors
sub AddVectors {
return ( $_[0] + $_[3], $_[1] + $_[4], $_[2] + $_[5] );
}
#------ Substract two vector
sub SubVectors {
return ( $_[0] - $_[3], $_[1] - $_[4], $_[2] - $_[5] );
}
#------ Returns the dot product of 2 vectors
sub DotProduct {
return $_[0] * $_[3] + $_[1] * $_[4] + $_[2] * $_[5];
}
#------ Returns the cross product of 2 vectors
sub CrossProduct {
return (
$_[1] * $_[5] - $_[2] * $_[4],
$_[3] * $_[2] - $_[0] * $_[5],
$_[0] * $_[4] - $_[1] * $_[3]
);
}
#------ Returns a normalized vector (length = 1)
sub NormalizeVector {
return ( 0, 0, 0 ) if ( my $norm = GetVectorLength(@_) ) == 0;
return ScaleVector( @_, 1 / $norm );
}
#------ Returns the length of a vector
sub GetVectorLength {
return sqrt( $_[0] * $_[0] + $_[1] * $_[1] + $_[2] * $_[2] );
}
#------ Returns the vector scaled by the last parameter
sub ScaleVector {
return ( $_[0] * $_[3], $_[1] * $_[3], $_[2] * $_[3] );
}
#------ Returns the distance between two points
sub Dist {
return GetVectorLength(SubVectors(@_));
}
#------ Returns the barycenter
sub GetBaryCenter {
croak "bad number of parameters in GetBaryCenter" if @_%4;
my ($xG, $yG, $zG, $s) = (0, 0, 0, 0);
while ( 0 < @_ ) {
my ($x, $y, $z, $k) = splice @_, 0, 4;
$xG += $k*$x;
$yG += $k*$y;
$zG += $k*$z;
$s += $k;
}
return $xG/$s, $yG/$s, $zG/$s;
}
#------ Returns the unit normal vector of a triangle specified by the three
# points P1, P2, and P3.
sub FindUnitNormal {
return NormalizeVector(
CrossProduct(
$_[0] - $_[3], $_[1] - $_[4], $_[2] - $_[5], # P1-P2
$_[3] - $_[6], $_[4] - $_[7], $_[5] - $_[8] # P2-P3
)
);
}
#------ Draw a circle in space
# We draw a circle in space as a torus with a small inner radius
# Usage: Drawcircle( $cx, $cy, $cz, $nx, $ny, $nz, $R [, $r]);
sub DrawCircle {
croak "bad number of parameters in DrawCircle" if 7 > @_;
my ( $cx, $cy, $cz, $nx, $ny, $nz, $R, $r) = @_;
$r ||= 0.04;
glPushMatrix();
my @axe = NormalizeVector CrossProduct(@k, $nx, $ny, $nz );
my $alpha = rad2deg acos(DotProduct($nx, $ny, $nz, @k ));
glTranslatef( $cx, $cy, $cz );
glRotatef( $alpha, @axe );
glutSolidTorus( $r, $R, 10, 100 ); # The circle!
glPopMatrix();
}
#------ Returns the angle ABC = (BA, BC)
sub GetAngle {
return acos(DotProduct( NormalizeVector(SubVectors(@_[0..2], @_[3..5])),
NormalizeVector(SubVectors(@_[6..8], @_[3..5]))
));
}
#------ Returns the circle circumscribed about a triangle
sub GetCircumCircle {
croak "bad number of parameters in GetCircumCircle" if 9 != @_;
my @A = @_[0..2];
my @B = @_[3..5];
my @C = @_[6..8];
my @N = FindUnitNormal( @A, @B, @C ); # normale
my $angleA = GetAngle( @B, @A, @C );
my $angleB = GetAngle( @A, @B, @C );
my $angleC = GetAngle( @A, @C, @B );
# the barycentric coordinates of the center
my @G = GetBaryCenter( @A, sin(2*$angleA),
@B, sin(2*$angleB),
@C, sin(2*$angleC));
return @G, @N, Dist(@G, @A);
}
#------ Returns the circle inscribed in a triangle
sub GetInCircle {
croak "bad number of parameters in GetCircumCircle" if 9 != @_;
my @A = @_[0..2];
my @B = @_[3..5];
my @C = @_[6..8];
my @N = FindUnitNormal( @A, @B, @C ); # normale
my $angleA = GetAngle( @B, @A, @C );
my $angleB = GetAngle( @A, @B, @C );
my $angleC = GetAngle( @A, @C, @B );
# the barycentric coordinates of the center
my @G = GetBaryCenter( @A, sin($angleA), @B, sin($angleB), @C, sin($angleC));
# find the radius
my $a = Dist(@B, @C);
my $b = Dist(@A, @C);
my $c = Dist(@A, @B);
my $s = ($a + $b + $c )/2;
my $r = sqrt( ($s-$a)*($s-$b)*($s-$c)/$s );
return @G, @N, $r;
}
#------ Rainbow color map function
# Usage: ($red, $green, $blue) = Rainbow( $x );
# $x must be between 0 and 1.
# Returns the color of the rainbow (RGB list) associated with $x
# from blue for $x = 0 to red for $x = 1.
sub max { $_[0] < $_[1] ? $_[1] : $_[0] } # max auxiliary function
sub Rainbow {
my $dx = 0.8;
my $s = ( 6 - 2 * $dx ) * $_[0] + $dx;
return max( 0, ( 3 - abs( $s - 4 ) - abs( $s - 5 ) ) / 2 ), # Red
max( 0, ( 4 - abs( $s - 2 ) - abs( $s - 4 ) ) / 2 ), # Green
max( 0, ( 3 - abs( $s - 1 ) - abs( $s - 2 ) ) / 2 ); # Blue
}
The script as .txt for download:
apollonius.pl.txt
Back to Top
BðP © 2013 J-L Morel - Contact : jl_morel@bribes.org
![[Validation HTML 4.0!]](vh401.gif)